Coronavirus Exercises Part 1

Determining a shape’s center of mass mathematically

In the main text, we noted that the center of some shapes can be computed mathematically. Consider the semicircular arc shown in the figure below, with endpoints (-1, 0) and (1, 0).

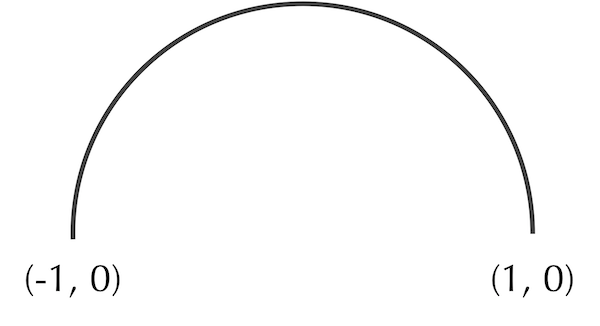A semicircular arc with radius 1 corresponding to a circle whose center is at the origin.

Exercise: Determine the center of mass of the shape in the figure above. (Hint: finding the x-coordinate of the center of mass is easy, but finding the y-coordinate requires a little calculus.)

Exercise: Say that we connect (-1, 0) and (0, 1) to form a closed semicircle. What will be the center of mass of the resulting shape?

Calculating RMSD

Consider the two shapes shown in the figure below with vectorizations of eight points each.

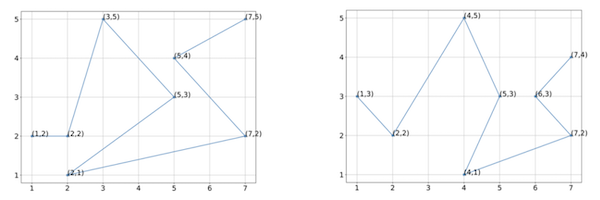Two hypothetical protein structures with vectorizations into eight points each.

Exercise: Using the vectorization of the figures indicated, estimate the center of mass of these two protein structures.

Exercise: Without rotating these structures, align the two structures so that they have the same center of mass, and determine the RMSD between the two structures for the vectorizations shown.

Practicing Ab initio and homology modeling

Let’s predict the structure of the beta subunit of human hemoglobin subunit alpha using both ab initio and homology structure prediction. To do so, first visit the Protein Data Bank and search for the protein “1SI4”. Download the PDB file by clicking on “Download Files” and then “PDB Format”. We will use this file for structure comparisons later. Next, go to the “Sequence” tab and click “Display Files” and then “FASTA Sequence”. In this file, find the sequence corresponding to the beta subunit.

Exercise: Submit the beta subunit sequence to the ab initio structure prediction software, QUARK as well as your choice of homology modeling software: SWISS-MODEL, Robetta, and/or GalaxyWEB.

In a tutorial, we saw how to use ProDy to compute RMSD between protein structures.

Exercise: Use ProDy to calculate the RMSD between your predicted structures from the previous exercise and the actual structure. (Use “Chain B” of the validated structure to focus on subunit beta.) Which type of modeling (ab initio or homology modeling) resulted in the most accurate structure prediction? Is this what you expected?

Trying out AlphaFold

A simplified version of AlphaFold is available for public use on Colab. This version currently does not work when using the entire spike protein, and so we will use the human hemoglobin subunit beta once again. Following the directions from a preceding exercise, obtain the protein sequence of the beta subunit. Next, open Colab’s simplified version of AlphaFold. Read the documentation and follow the directions in each step to generate a predicted structure.

Exercise: Use ProDy to calculate the RMSD between the predicted structure and the actual structure. Did this simplified version of AlphaFold perform better than your ab initio and homology modeling results from the previous exercise?